
When Ramanujan did mathemagic with a taxi number
As he rummaged through the yellowing old pages in a box full of loose sheets, Ken Ono froze. His heart stopped a beat. A scribble at the corner of the page attracted his attention. The handwriting was familiar and its content was startling.

As he rummaged through the yellowing old pages in a box full of loose sheets, Ken Ono froze. His heart stopped a beat. A scribble at the corner of the page attracted his attention. The handwriting was familiar and its content was startling.
A mathematician at Emory University, Ono was the math consultant for Dev Patel and Jeremy Irons who acted in the Hollywood movie, The Man Who Knew Infinity.
He and number theorist Andrew Granville were at the Ramanujan archive at Cambridge. “From the bottom of one of the boxes, I pulled out this sheet,” recalls Ono. On the right bottom corner of the page, in the characteristic handwriting of Ramanujan were two equations: 1^3 + 12^3 and 9^3 + 10^3.
The solution to both the equations is 1729.
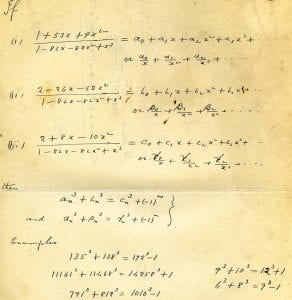
Before his eventual return to India, and the subsequent tragic death, Ramanujan was seriously ill and was admitted to a hospital in England. Ramanujan was in a dilemma. He longed to be with his wife, Janaki, and missed her home-cooked food.
He knew, leaving England to India would cost his progress in mathematics. His attempt to bring his wife to England met with failure. His mother put her foot down, saying Janaki will be a distraction to Ramanujan’s mathematics. His mother reasoned that vile Englishmen, in Ramanujan’s absence, may seduce Janaki.
Meanwhile, domestic discard had flared between Janaki and Ramanujan’s mother, resulting in both not writing to him as often as earlier. His illness was also a riddle. While most doctors diagnosed him to be suffering from tuberculosis, his body did not respond to any of the treatment. Moreover, the British climate was not conducive.
Added to the misery, the onset of the First World War meant rationing as well as stoppage of postal parcels with foodstuff from Madras that had been sustaining Ramanujan. Just a few months earlier, he had been elected member of Royal Society and given a fellowship in Trinity College. He had also made a suicide attempt by jumping before a London metro. Ramanujan was at the same time elated and despondent.

Godfrey Harold Hardy, the English mathematician, was Ramanujan’s mentor at Cambridge. Although Hardy was a shy and cold person, he had a special place for Ramanujan. Wanting to cheer up the dejected Ramanujan ailing in a clinic near London, Hardy wanted to strike a conversion. Later Hardy recollected that incident.
“I remember once going to see him [Ramanujan] when he was lying ill at Putney. I had ridden in taxicab No. 1729 and remarked that the number seemed to be rather a dull one and that I hoped it was not an unfavourable omen.”
“No,” he replied, “it is a fascinating number; it is the smallest number expressible as the sum of two [positive] cubes in two different ways.”
1^3 + 12^3 = 1 + 1,728 = 1,729
9^3 + 10^3 = 729 + 1,000 = 1,729
Amazed at the answer, Hardy asked if he knew the corresponding result for fourth powers. The smallest integer that can be written as a sum of two fourth powers of integers in two ways. After thinking for a moment, Ramanujan replied in negative. However, he said such a number must be huge. Indeed it is a very large number:
133^4+134^4= 158^4+59^4= 635,318,657.
This incident launched the ‘Hardy-Ramanujan number’ or ‘taxicab number’ into the world of math. Taxicab numbers are the smallest integers which are the sum of cubes in n different ways. The first taxicab number is simple 2 = 1^3+1^3. The second is 1729, which can be written as the sum of two cubes in two different ways.
The third taxi cab number is 87539319, the smallest number that is equal to the sum of two cubes in three different ways. The fourth one is the sum of two cubes written in four different ways. To date, only six taxicab numbers have been discovered.
Enigma
Often tales are told to give an impression that Ramanujan comes up with unusual properties of number by sheer intuition. Frequently, his work is presented as a curiosity, an inconsequential piece of recreational mathematics.
It is not such a big surprise that Ramanujan knew that 1,729 is the sum of two cubes in two different ways. Since Ramanujan was from India, which used imperial measures at the time, he would probably have been taught at school that there were 1,728 cubic inches in a cubic foot. He would also have known that 729=9^3. But how he knew that it was the smallest?
Properties of 1,729 were not unknown to Ramanujan. He had written it down before even coming to England. Not once, but thrice Ramanujan had recorded properties of 1,729 in his famous notebooks much before the taxicab incident. Therefore, his quick response to Hardy at the hospital was not something he computed at the spur of the moment, but something he recalled from his earlier works.
Related News: What simple mathematics can tell us about coronavirus
In his second notebook, in the chapter XVIII, the case is given as a single worked out example of an infinite family of solutions for the Diophantine equation of the form x^3+y^3=u^2 and Euler’s equation x^3+y^3+z^3=u^3.
Ramanujan provides six numerical illustrations for the first and 12 for the second. The second of the 12 examples for Euler’s equation is the famous 1^3+12^3=9^3+10^3 (=1,729). This also finds a place in questions and solutions submitted by Ramanujan to the Journal of the Indian Mathematical Society.
Once in 1913, as a solution to the identity:
(6A^2−4AB+4B^2)^3 = (3A^2+5AB−5B^2)^3+(4A^2−4AB+6B^2)^3+(5A^2−5AB−3B^2)^3.
Dividing both sides by 27, Ramanujan arrives at s 12^3 = (−1)^3 + 10^3 + 9^3. Again in 1915 (question no. 681, vol VII page 160), he seeks the solution in integers for the equation x^3+y^3+z^3=1. He asks the readers to deduce 9^3+10^3=12^3+1 from the general solution to the identity.
What Ono had stumbled upon was the fourth entry of this now-famous number, until then unnoticed. This entry was after the taxicab incident. Perhaps, Ramajuan revisited the explorations in this area of number theory kindled by the hospital episode.
Lost and found ‘the last notebook’
Given his health, mental condition and the grim situation resulting from the outbreak of the First World War, Hardy decided that returning to India was the best option for Ramanujan. Hardy made arrangements and Ramanujan returned to India emaciated. Since his return, until his death on April 22, 1920, his wife Janaki took care of him.
Even while recouping, Ramanujan continued his mathematical explorations. Janaki recalled how Ramanujan used to claim that mathematics was his distraction from the pain and sufferings. He wrote theorems and formulas like there was no other day. After Ramanujan died, the young widow Janaki collected the three notebooks and sheaf of papers and submitted them to the University of Madras.
The University made a copy of these papers and a set to Hardy who was then embarked upon producing a posthumous volume on Ramanujan containing published documents, notebooks, and other unpublished work. Hardy in association with P. V. Seshu Aiyar came out with a Collected Papers of Srinivasa Ramanujan.
Related News: A century later, why the world still needs Ramanujan
Subsequently, Hardy passed on the manuscripts, letters, and notes to G.N. Watson, an eminent mathematician, who came out with 40 papers in the 1920s and 30s. After the death of Watson, the manuscripts remained lodged in Wren library, all but lost, languishing unread for more than 50 years.
While examining the estate of the late G.N. Watson, G.E. Andrews in 1976 accidentally found a box full of manuscripts in Ramanujan’s distinctive handwriting. It contained about a hundred pages, with 138 sides and over six hundred mathematical formula without proofs.
Although technically it was not a notebook, this is the now called the ‘last notebook’. Once rediscovered, it opened a flood of new ideas in the world of mathematics, most notable being the mock theta functions.
More than meets the eye
Ono and Andrew were amused at first to see the 1+12^3=9^3+10^3 scribbled in a corner. Their immediate reaction could have been just curiosity on this oddity. On careful reading of the sheet, Ono found a set of equations. These equations were familiar, they had the likeness of Fermat’s last theorem. Ramanujan had been working on this grand seventeenth-century problem.
“The page mentioned 1,729 along with some notes about it. Andrew and I realised that he had found infinitely near misses for Fermat’s Last Theorem for exponent 3. We were shocked by that,” says Ono.
Pierre de Fermat was one of the most renowned number theorists ever, but was too lazy to publish. We come to know much about his work from the letters and notes he had left. Like Ramanujan, he was cryptic, and hardly showed the proof. Mathematicians, proved one after another the claims of Fermat, except one.
Called Fermat’s last theorem, it stated that x^n + y^n = z^n has no non-zero integer solutions for x, y and z when n > 2, remained a riddle for hundreds of years. In the margins of his copy of Diophantus’s Arithmetica, Fermat in 1637 had confidently scribbled, “I have discovered a truly remarkable proof which this margin is too small to contain.”
It took numerous mathematicians, several years of research before British mathematician Andrew Wiles came up with a proof in 1995 which was 129 pages long! Surely that would not have fitted the margins of the page.
Elliptic curves
If only one can find one x,y,z such that x^3+y^3=z^3; the counter-example will prove Fermat wrong. We never know if Ramanujan was trying to prove Fermat wrong, but it is evident that he was computing near misses, that is solutions that are off only by plus or
minus one.
By finding integer solutions for formulas x^3+y^3=z^3+1 or = z^3-1 he dwelled deeper into what is called as ‘elliptic curves’. One of the near misses, Ramanujan offered was the familiar 1+12^3=9^3+10^3. Ellipses and elliptic curves are distinct. Circles, ellipses and families of curves are what are called as conical curves. They are curves that can be obtained by slicing a cone in different ways. Elliptic curves are graphs in a plane that has no cusps or self-intersections.
Recall your high school mathematics. The equation x^2+y^2=r^2 represents a circle with radius r. Likewise, an equation x^3+y^3=z^3+w^3 in our modern perspective gives a rational elliptic surface. In his deathbed, Ramanujan had worked out infinite families of solutions to these curves. All trying to figure out Fermat’s last theorem.
Deep intuition
Ono knew he had hit the jackpot. Once he returned to Emory University, he worked on the
leads with his PhD student. “Together with my PhD student Sarah Trebat-Leder, we discovered that these identities can be reformulated as statements about two important areas of mathematics that did not even exist in Ramanujan’s day,” says Ono.
Ono and Sarah Trebat-Leder worked backwards to figure out his secret. Ramanujan had arrived at the formulae on that page by generating a more general identity. Ono recognised that the more general identity was an exceptional K3 surface, an exotic mathematical object.
In wonderment, Ono says, “mathematicians did not discover K3 surfaces until the 1960s, yet Ramanujan had already worked on it forty years before!” Using Ramanujan’s insights, Ono and Trebat-Leder were able to provide numerous examples of a particular category of an elliptic curve, far beyond anyone had done.
“It turns out that Ramanujan’s work anticipated deep structures and phenomena which have become fundamental objects in arithmetic geometry and number theory,” says Ono.
The legacy
From exploring the quantum world to secure internet transactions, Ramanujan’s legacy plays a role. K3 surfaces and rank of elliptic curves, two prominent subjects are hot topics today. They are indispensable mathematical tools for string theory and cryptography, respectively.
We are familiar with the three space dimensions (up-down; left-right and forward- backwards) and the fourth time. Curiously the string theory, if true, says that the world we live in consists of more than the three spatial dimensions that we perceive. Like the ant crawling on the surface of the ball never comprehend the third dimension, the extra dimensions proposed by the string theory are folded up tightly into too small space for us to perceive.
For that, the tiny wrapped spaces must have a particular geometric structure, called Calabi-Yau manifolds. K3 surfaces, which Ramanujan was the first to discover, are the simplest classes of Calabi-Yau manifolds. The enigmatic K3 surfaces are named in honour of Kummer, Kähler and Kodaira, three mathematicians who had done much of the pioneering work in this area during the 1950s.
Modern-day cryptography involves a public key used for encryption the plain text into cypher text and another key called the private key, used by the receiver to decrypt the ciphertext to read the message and a trapdoor algorithm. Multiplication of two prime numbers is easy, however finding their prime factor is very tough. The trapdoor algorithms use such processes where it is accessible in one direction (encryption), hard the other
(decryption).
Amazingly, a straight line intersecting an elliptic curve at two points uniquely intersects at a third point. This unique property of the elliptic curves is exploited to build modern-day Elliptic Curve Cryptography (ECC) that secures our internet transactions. Ramanujan passed away a hundred years ago. Yet his work inspires generations of mathematicians.

