
Ramanujan's enchanting journeys in the maze of 'continued fraction'

One Sunday morning of December 1915, tucked with the latest issue of monthly Strand Magazine, Prasanta Chandra Mahalanobis stormed into Ramanujan’s room at the Trinity College, London. They had agreed to meet for lunch.
Mahalanobis had arrived in England in 1913 and joined King’s College, Cambridge, one year before the arrival of Ramanujan. Later, Mahalanobis would become a renowned statistician best remembered for Mahalanobis distance, a statistical measure and for his contribution to the design of large-scale sample surveys. He founded the Indian Statistical Institute and was the main driver behind the first Planning Commission of Independent India.
Before we proceed further to describe the eventful Sunday, let us take a detour. How Ramanujan met Mahalanobis and each developed a close friendship at Cambridge is a charming story. Soon after the arrival of shy and reserved Ramanujan, Mahalanobis visited him at his room in Trinity College. It was a cold day, and Ramanujan was sitting very near the fire.
Solicitously, Mahalanobis asked him, “are you warm at night.”
“No, it is unbearably cold,” Ramanujan said. “I sleep with my overcoat and wrap myself in a shawl.”
Mahalanobis was aghast. He thought, perhaps, the usher had not provided adequate blankets to Ramanujan. Mahalanobis inspected the bed. He was startled. The bed was as it was made. There were indeed several blankets, all but tucked tightly. A bed cover was spread over them.
Alas, Ramanujan, coming from South India, used to sleep on the floor on a mat. He was not aware of how to turn back the blankets and get into the bed. All these days, Ramanujan was sleeping under the loose bed cover with an overcoat and shawl. Mahalanobis taught him how to go under the blankets. Ramanujan was incredibly touched. This minor incident made them lifelong friends. Since then, it became customary for both of them to meet on Sunday mornings and take long walks, as long as they were in Cambridge.
The puzzle
That Sunday, Mahalanobis was invited by Ramanujan for lunch. Stirring vegetables in a pan over the fire, Ramanujan was busy in the kitchen. Nothing to do before the lunch is ready, Mahalanobis was turning the pages of the magazine he had brought. One page captivated him. His attention was arrested. Mumbling to himself, Mahalanobis immersed himself in calculations.
Written by Henry E. Dudeney, ‘Puzzles at a Village Inn’ posed a recreational mathematics problem. The puzzle itself was about a street in the town of Louvain in Belgium. The puzzle read:
“I was talking the other day,” said William Rogers to the other villagers gathered around the inn fire, “to a gentleman about the place called Louvain, what the Germans have burnt down. He said he knew it well — used to visit a Belgian friend there.
He said his friend’s house was in a long street, numbered on this side one, two, three, and so on, and that all the numbers on one side of him added up precisely the same as all the numbers on the other side of him. Funny thing that! He said he knew more than fifty houses on that side of the street, but not so many as five hundred. I made mention of the matter to our parson, and he took a pencil and worked out the number of the house where the Belgian lived. I don’t know how he did it.”
Perhaps the reader may like to discover the number of that house.”
Along a long road in that town, one British officer was lodged. Suppose let us say there are total ‘x’ houses on the road and the house number of the officer was ‘h.’ Each home in the street was consecutively numbered, without any number missing in between. A second officer came to meet them. He started his journey from the beginning of the road and added the door number of houses on his way till he reached the first officer’s home. That is, he summed the numbers from 1 to (h-1). After meeting the first officer and spending some time with him, the second officer proceeded to the other end of the road. While going towards the other end of the road, he added the number of houses until the last place. He started from h+1 and continued to add till ‘x’, the terminal house number. To his utter surprise, the second officer found that the total of the numbers was the same as he got before when he arrived at the first officer’s house.
That is the sum 1+ 2+ 3+ … + (h-1) is same as the sun (h+1) + (h+2)… +x. How many houses are there in the street (that is the value of x), and what is the house number of the British officer (that is the value of h).
This is not that difficult. With trial and error, we can hit upon an answer. For example, if the street had 8 houses, the officer stayed at house number “6.”
| 1+2+3+4+5 | = | 7+8 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
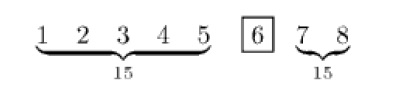
We can see that 1+2+3+4+5 = 15, so is 7+8.
The puzzle in the magazine was not this simple. It said there were more than 50 and less than 500 houses. Mahalanobis had to use the trial-and-error method, but it was not that simple.
Mahalanobis recalls, “It was not at all difficult. I got the solution in a few minutes by trial and error.” The answer is 288 houses in the street, and the door number of the officers’ house is 204.
That is 1+2+3… +203 = 205+206+…288. You can verify and check for yourself.
Having got the answer, Mahalanobis wanted to amuse Ramanujan. Playfully, Mahalanobis said, “Ramanujan, nowhere is a problem for you.”
Still facing the oven and stirring the pan, Ramanujan asked, “what problem?”
Mahalanobis read out the question from the Strand magazine. Even before Mahalanobis fished reading, Ramanujan retorted. “Why have the restriction between 50 and 500, I shall give you solution for all cases; please take down the solution.’ Ramanujan proceeded to give off a series of solutions.
The first 10 solutions are :
| SlNo | House number (h) | Total houses in the street (x) | Implication |
| 1 | 0 | 0 | Trivial |
| 2 | 1 | 1 | 1=1 |
| 3 | 6 | 8 | 1+2+..5 = 7+8 |
| 4 | 35 | 49 | 1+2+3+…34 = 36+37+…49 |
| 5 | 204 | 288 | 1+2+3+…203 = 205+206+…288 |
| 6 | 1189 | 1681 | 1+2+3…+1188 = 1190+1191+..1681 |
| 7 | 6930 | 9800 | |
| 8 | 40391 | 57121 | |
| 9 | 235416 | 332928 | |
| 10 | 1372105 | 1940449 |
Amazed Mahalanobis asked, “How did you get this solution in a flash.”
“As soon as I heard the problem, it was clear to me that the solution was obviously a continued fraction; I then scratched my head, ‘Which continued fraction?’ and the answer came to my mind. It was just as simple as this.”
Mahalanobis was speechless; a hundred years later, anyone who hears this story is most likely to disbelieve. How could he find the right continued fraction in a jiffy? Amazing, indeed.
Solving the puzzle
Recall the mathematical formulation of the puzzle: 1+2+3+…(h-1)= (h+1)+(h+2)…+x; where ‘h’ is the house number and ” is the total number of houses in the street.
From our high school maths, we know 1+2+3+4.. +n is n(n+1)/2. Using the above, we know
1+2+3+…(h-1) = (h-1)h/2
and
(h+1)+(h+2)…+x = (x(x+1)/2) – (h(h+1)/2)
but 1+2+3+…(h-1)= (h+1)+(h+2)…+x
Therefore:
(h-1)h/2 = (x(x+1)/2) – (h(h+1)/2)
or
(h2-h)/2 = [(x2+x)/ 2 ] -[(h2+h)/2] rearranging we get
h2= x(x+1)/2,
For various values of h, the value of h2 is a square number. That is the series 1, 4, 9 16, 20, 36, 49 …and so on.
For various values of x, [x(x+1)/2] is 1, 3, 6, 10, 15, 21, 28, 36, 45, 55… and so on. That is triangle numbers series.
If h2= x(x+1)/2, means h2 is not only a square but also a triangle number. The value of h is such that it must be in the sequence of squares and a series of triangle numbers.
Compare the two sequences. The first two common numbers of 1, 36, correspond to the h-1 and h=6.
When h= 1, h2= x(x+1)/2 yields x= 1
When h = 6, h2= x(x+1)/2 yields x= 8 ( 36 is 8th in the triangle number series)
That is if values of ‘h’ for which the formula h2= x(x+1)/2 has integer solution can be identified, using the formula for solving simple quadratic equation x2+x-k=0, solution for x can be found.
From the first two solutions for ‘he, being 1 and 6, Ramanujan perhaps formulated the following continued fraction:-
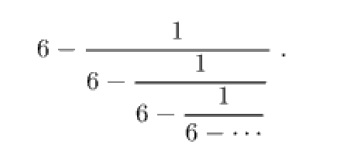
The truncated partial sums of this continued fraction are
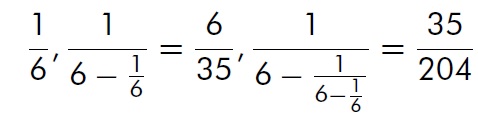
and so on.
Look at the series of the denominators (or numerators) of these partial sums. They are 6, 35, 204, 1189, and so on. They are the house numbers ‘h’ in the puzzle! Now, for an careful observer the series of ‘h’, 1, 6, 35, 204, 1,189, 6930 has an interesting pattern. The solution 1 is trivial case. The next one 6 can be arrived easily. (6X6) -1 = 35; (6×35) -6=204; (6x 204) 35=1189; (6X1189) 204 =6930. The 7th term in this series would be 40391 which is (6×6930) – 1,189. Once you have the value for ‘h’, the corresponding value for ‘x’ can be computed by the formula h2= x(x+1)/2. Once you get the continued fraction, computing the values becomes simpler.
| Term | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| The house number (h) | 0 | 1 | 6 | 35 | 204 | 1,189 | 6,930 |
| Total houses in the street | 0 | 1 | 8 | 49 | 288 | 1,681 | 9,800 |
A gentle introduction to continued fraction
But what is this animal called ‘continued fraction?’ It is a fantastic way of representing real numbers. Any number that can be written as a ratio of two integers that is a fraction is rational. A fraction can be written in the form of decimal expansion. That is, rather than write ½, we can represent it as 0.5.
Trivially, we can write whole numbers as fractions as well as decimals. For example 143= 143/1= 143.0 That is it. Now we can write ¼ as 0.25 and likewise 3/40 as 0.075 and so on.
Now take the fraction 3/41. If we write this in decimal form, this is = 0.0731707317073170731707317073170…
We know 10/3 is = 3.333… The ‘3’ recurs in this decimal expansion. However in 1/7= 0.142857142857… ‘142857’ recurs periodically.
Whole numbers such as ‘5’, numbers that have finite decimals, such as ‘0.5’ and those which have never-ending but repeating patterns, such as ‘3.333…’, in the decimals are ‘rationals’.
The rational numbers are the ones we know best. Astonishingly rational numbers are actually rare among all real numbers! Then there are a new class of numbers that are mysterious, puzzling. When they are written in decimals, they are not only continual but never repeating.
They cannot be written as fractions, a ratio of two integers.
From our high school mathematics, we know that √2 is ‘irrational’; it cannot be expressed as the ratio of two integers. Its decimal expansion is non-terminating and non-recurring.
Often we take the value of √2 = 1.414; however, we must know that this is an approximate and not precise value.
√2= 1.414213562373095048801688724209698078569671875376948073176679737990732
is the first ‘seventy’ decimal expansion of √2. Modern computers have been deployed to compute the first million digits, and there are no repeating patterns. In short, when there is no repeating pattern in the decimal expansion, the number is ‘irrational’.
Rational and irrational numbers, put together, are called ‘real’ numbers. In addition to decimal expression and fractional form, there is a third way to represent any real number (both rational and irrational) which is mathematically known as continued fractions.
Trivially a whole number such as 19 can be written in a fractional form = 1/(1/19) and a negative ‘integer’, say -23, can be expressed as = -23/1 = – 1/ (1/23). This may seem convoluted. However, this form has a lot to offer when the real numbers are irrational or transcendental.
Suppose we want to express a rational fraction like 72/28. We can do so as follows.
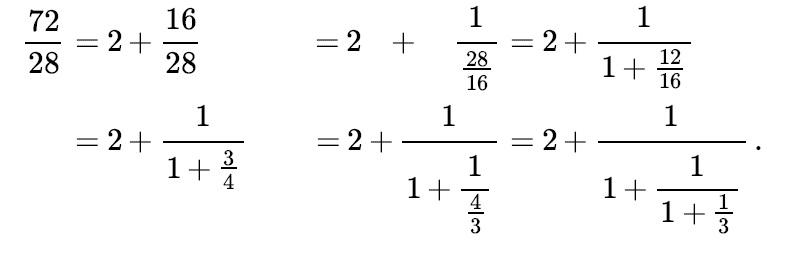
This means 72/28 is =
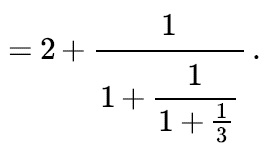
Likewise, let us do it for another rational number, 43/30

Given a continued fraction of a rational number, we can also sum it and find the value. See this case.
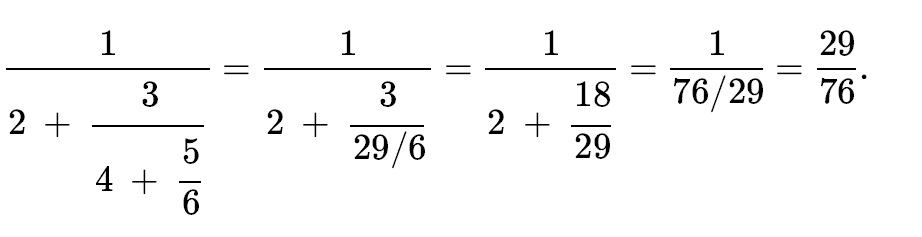
Reasoning the irrationals
We know from our high-school mathematics that irrationals like √2 cannot be written as a fraction of two whole numbers. However, continued fraction gives a way of elegantly handling irrationals.
Suppose x=√2, it means x^2-2=0
we can write this as x^2-1=1
or as x^2-1^2=1
(x+1)(x-1)=1
x-1= 1/(x+1)
x= 1+ [1/(x+1)]
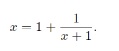
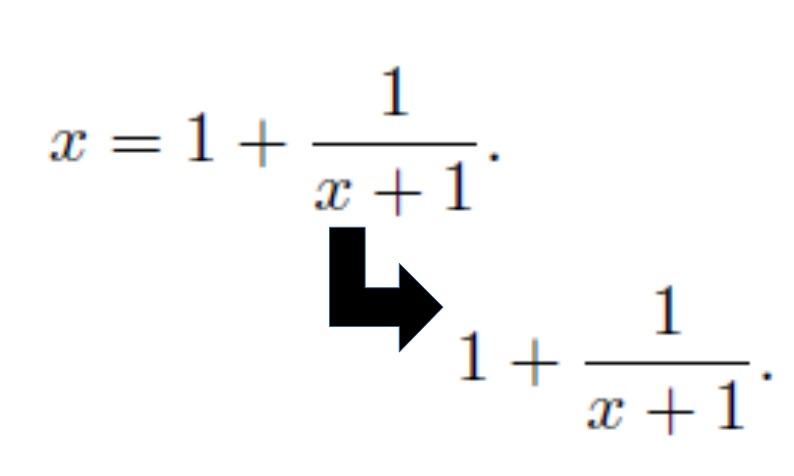
Observe, 1+1/(x+1) is same as x. We can replace on the left-hand side the x with 1+1/(x+1). Now, this becomes:-
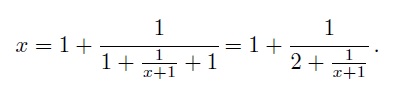
If we continue this recursively, we get
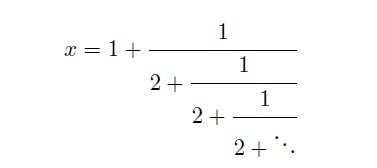
Recall x=√2. Therefore, we get:-
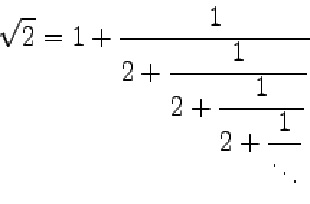
In the above notation, the “…” imply infinite recursion.
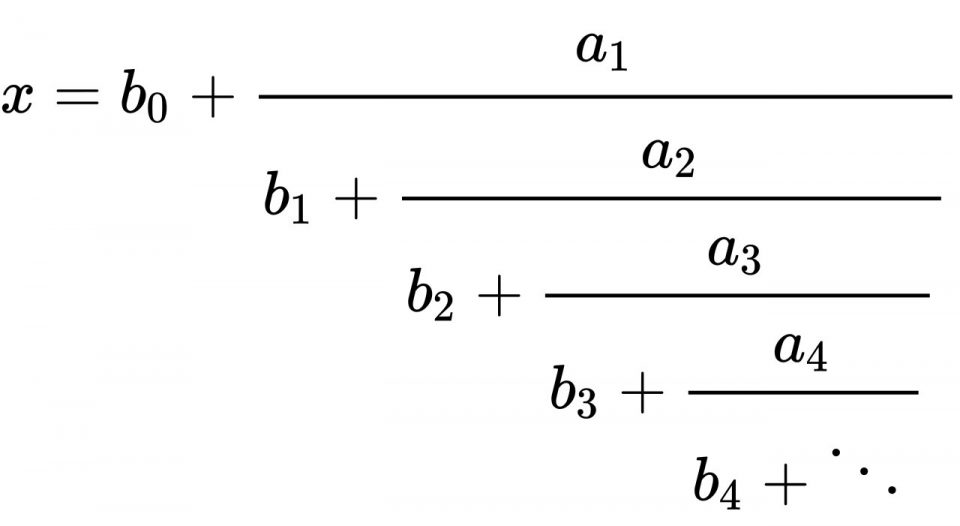
In fact, any real number ‘r’ can be expressed in this ‘continuous’ fraction.
Where all the ‘a’ and ‘b’s are integers.
At first glance, the continued fractions may appear grotesque. Nevertheless, elegance is revealed if you look deeper into it. Try taking the truncated partial sums of the above.
Let us take the case of √2. It is an infinite series. Let us find the successive truncated sums.
For example first truncation = 1/1 = 1
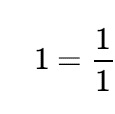
Second truncated sum = 1/ 2+ (1/1) which is = 3/2
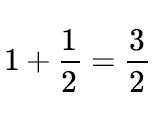
The third truncated sum is = 7/5
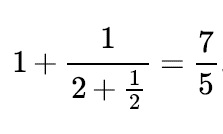
The fourth truncated sum is = 17/12
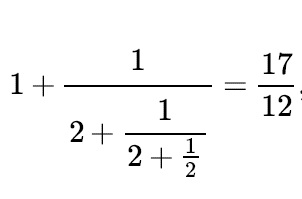
The series of truncated partial sums of the above-continued fraction will yield a value of
1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985 , 3363/2378 …and so on.
Each of these gives an approximate value of √2 with increasing precision!
But one may feel a bit dizzy computing the partial sums from the continued fractions. However, there too, a beautiful pattern is hidden.
Look at the pattern in the numerator of the above partial sums.
The numerators are
3= 1+2
7=2+5,
17=5+12,
41= 12+29… The numerator is the sum of its denominator and the previous term’s denominator.
Now you can also see a pattern in the denominators beyond the third partial sum.
12= (2×5)+2; 29= (2×12)+5, 70= (2×29)+12. That is the denominator is twice its previous denominator plus the one before!
The continued fraction provides an easy way of computing the increasingly better approximate value for irrational numbers.
The beauty of continued fractions
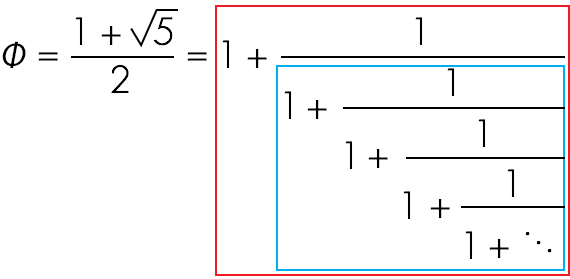
Ramanujan was a world expert on continued fractions. He found exquisite expressions for the golden ratio, the number phi; which, he found was nothing but one plus one divided by one plus one divided by, and you go on forever.
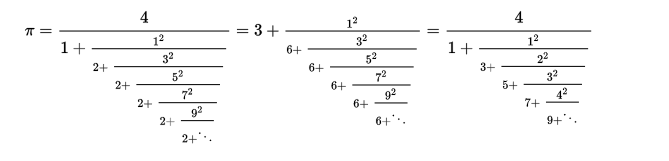
 Ramanujan’s publication, titled “Modular Equations and Approximations to π”, which he wrote in 1914, contained seventeen different elegant series that converged rapidly to π. According to him, the the value of π can be expressed as continued fractions with remarkable patterns.
Ramanujan’s publication, titled “Modular Equations and Approximations to π”, which he wrote in 1914, contained seventeen different elegant series that converged rapidly to π. According to him, the the value of π can be expressed as continued fractions with remarkable patterns.
In addition to being a very efficient process for finding the best rational approximations of transcendental numbers such as Pi or irrationals such as root 2, continued fractions are a versatile tool for solving movements involving two different periods. Typically, the stars orbit around the galaxy and wobble up and down through the galaxy’s plane. These two oscillations are often irrational numbers resulting in a non-periodic motion. The continued fractions shed enchanting illuminations on these chaotic motions.


